

To motivate this class, consider an econometric model whose. Then we discuss loss functions, risk, bias, and variance2.

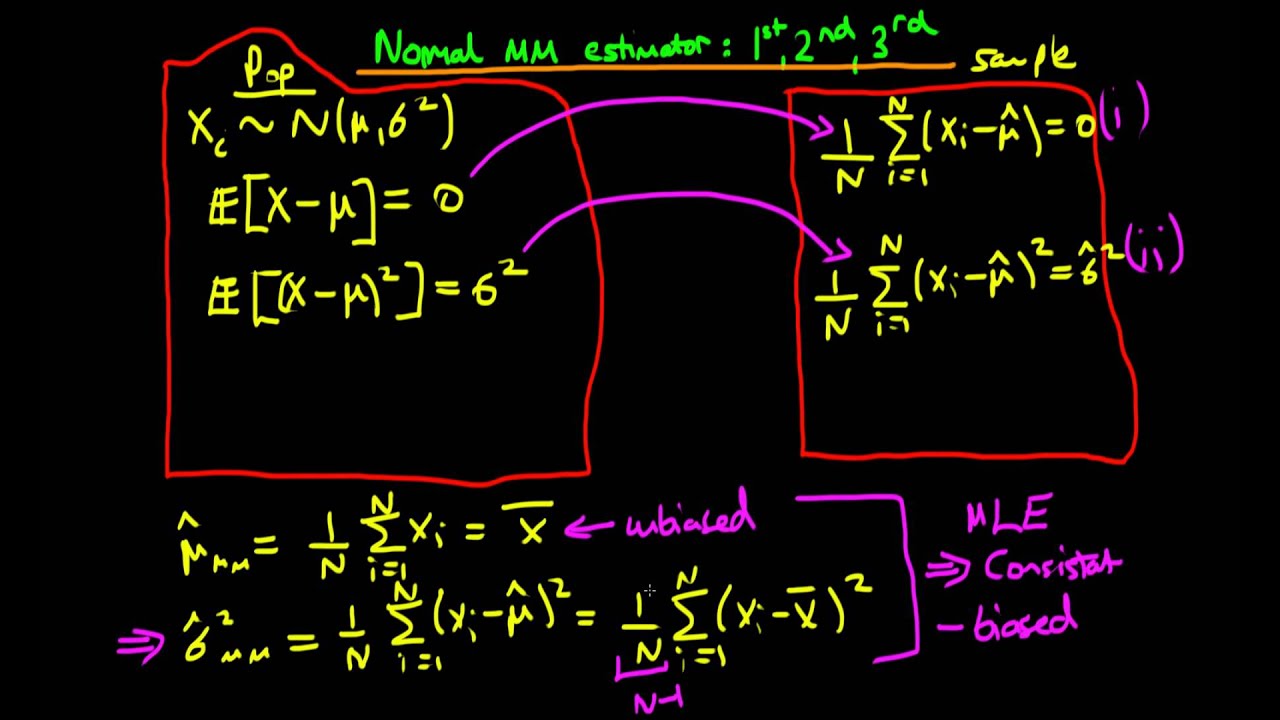
Introduction We start with de nitions related to estimation1. The result looks like this (apologies for the lack of refinement in this quick graph, cutting off part of the top):Īt least visually, it seems to be a pretty good fit.įor standard errors etc., a method for the generic function vcov() is provided: > gmmout vcov(gmmout) method of moments (GMM) estimators which subsumes many standard econo- metric estimators. Method of Moments MATH 667-01 Statistical Inference University of Louisville SeptemLast modi ed: 1/19 Lecture 5: Point Estimation, Bias, and the Method of Moments. Let’s specify momentftn: g gmm(g,x,c(alpha=0.1,beta=0.1)) Where data is our data in matrix or vector form, momentftn specifies the moments, and start is our initial guess for the iterative solution process. In our elementary usage here, the call form is gmm(data,momentftn,start) Expressions are obtained for the second and third moment about the mean, and the theory is applied to three cases of interest. Yet another tribute to the vast variety of packages available on CRAN! Of course, the solution part may not be so simple, due to nonlinearities, but gmm worries about all that for us. MM is a model of simplicity - we match these to the sample mean and variance of our data, and then solve for α and β. Secondly, we introduce a method of moments for estimating the unknown parameter, the description of the method is presented as follows. That makes it a candidate for fitting a beta distribution.ĭenoting the parameters of that family by α and β, the mean and variance are α / (α + β) and α β / ((α + β) 2 (α + β + 1)), respectively. The method of moments estimator of 0 is obtained by replacing the population mo ments by sample moments and solving for ,i. The method of moments isbasedonknowingtheformofuptop moments of a variable y as functions of the parameters, i.e. The first column of this data frame, brozek, is the percentage of body fat, which when converted to a proportion is in (0,1). GMM being a generalization of the classical method moments. Method of moments estimators: It can be referred to as a method of estimating the parameters of the population.
Our data set will be bodyfat, which is included in the mfp package, with measurements on 252 men.
#Method of moments how to#
CRAN has a package gmm that does MM, actually the Generalized Method of Moments, and in this post I’ll explain how to use it (on the elementary level, at least). If the model has d parameters, we compute the functions k m in equation (13.1) for the rst d moments, µ 1 k 1( 1, 2. Our estimation procedure follows from these 4 steps to link the sample moments to parameter estimates. MM has always been a favorite of mine because it often requires fewer distributional assumptions than MLE, and also because MM is much easier to explain than MLE to students and consulting clients. The method of moments results from the choices m(x)xm. An almost-as-famous alternative to the famous Maximum Likelihood Estimation is the Method of Moments.


 0 kommentar(er)
0 kommentar(er)
